Term Projects

Linear theory of Faraday instability in viscous fluids
Advisor: Prof. Krishna Kumar, Department of Physics, IIT Kharagpur | -
For the course Fluid Mechanics in my 4th semester, in this project I studied the
onset of Faraday Instability, i.e eventual ramp up of surface wave patterns in a fluid being oscillated vertically. For this I first linearized the
Navier-Stokes variant for the surface displacement field then took the spatial Fourier transform. In the Fourier space now I used Floquet analysis
to get the dynamics of the continuum of modes. Finally by reduction of the dynamics to a finite discrete set of Fourier modes, thereby represting it by a matrix, I computed
the instability diagrams via the eigenvalues.

Shadows of Black Holes and Rendering an Image of the Accretion Disk
Advisor: Prof. Sayan Kar, Department of Physics, IIT Kharagpur | -
When black holes are observed using any of imaging techniques, there is always a dark region often incorrectly labeled as the event horizon. This is related to the fact that light emitted at certain angles even at certain distances away from the event horizon, do fall back into the horizon. This leading to a circular dark region larger than the event horizon is called the shadow of black hole. In this project, for the course: General Theory of Relativity, taken in 6th semester, the null geodesics for different impact parameters are studied analytically using EOMs and conserved quantities derived from the Schwarzchild's metric. The EOMs were used to numerically simulate the light paths emitted from the accretion disk and projected upon camera's image plane at different angles to render the images shown in the right.

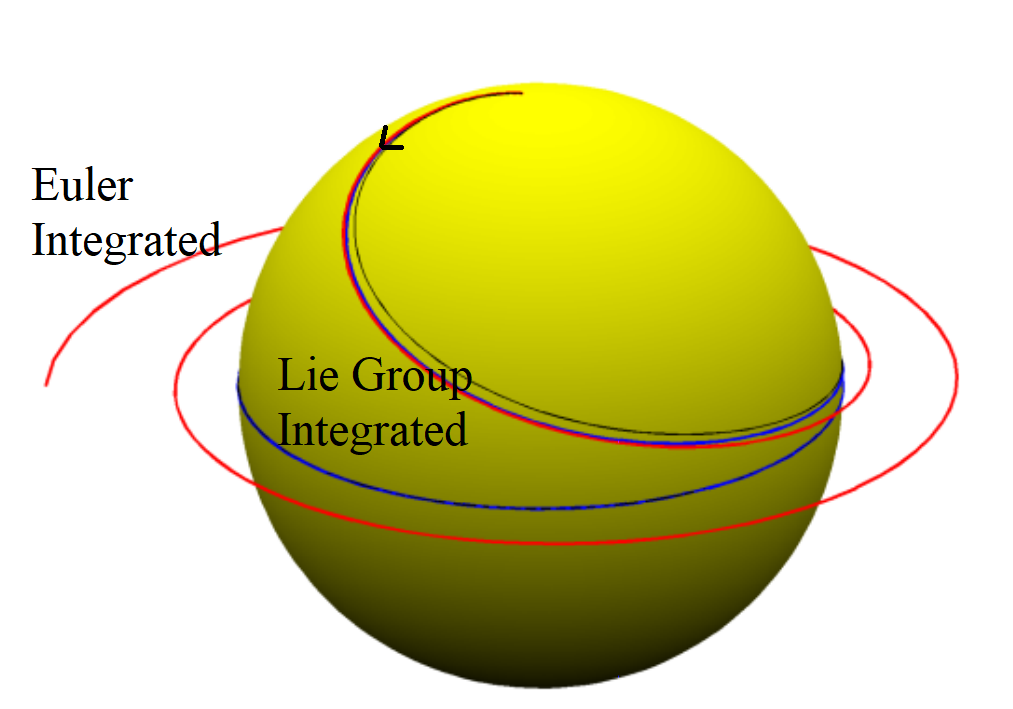
Lie Groups: Geometry of Dynamics and Geometry Preserving Simulators
Advisor: Prof. Jyotirmoy Bhattacharya, Department of Physics, IIT Kharagpur | -
The dynamics of systems are usually charecterized by the hard constraints they obey and that assigns a specific manifold to the configuration space of the system, like a circle for a pendulum, 2-torus for a double pendulum etc. If we simulate these system with conventional Euler based methods then the increments in time will always push the system away from the assigned manifold and this is where the Lie Group Integrator enter. In this essay, part of Mathematical Methods-2 course taught in 6th semester, I make an attempt to show how time evolution of dynamical systems can be thought as action of a Lie Group element on state space. As an example I simulate an SO(3) system showing that it preserves the group symmetry 1013 times better than Eulerian methods.

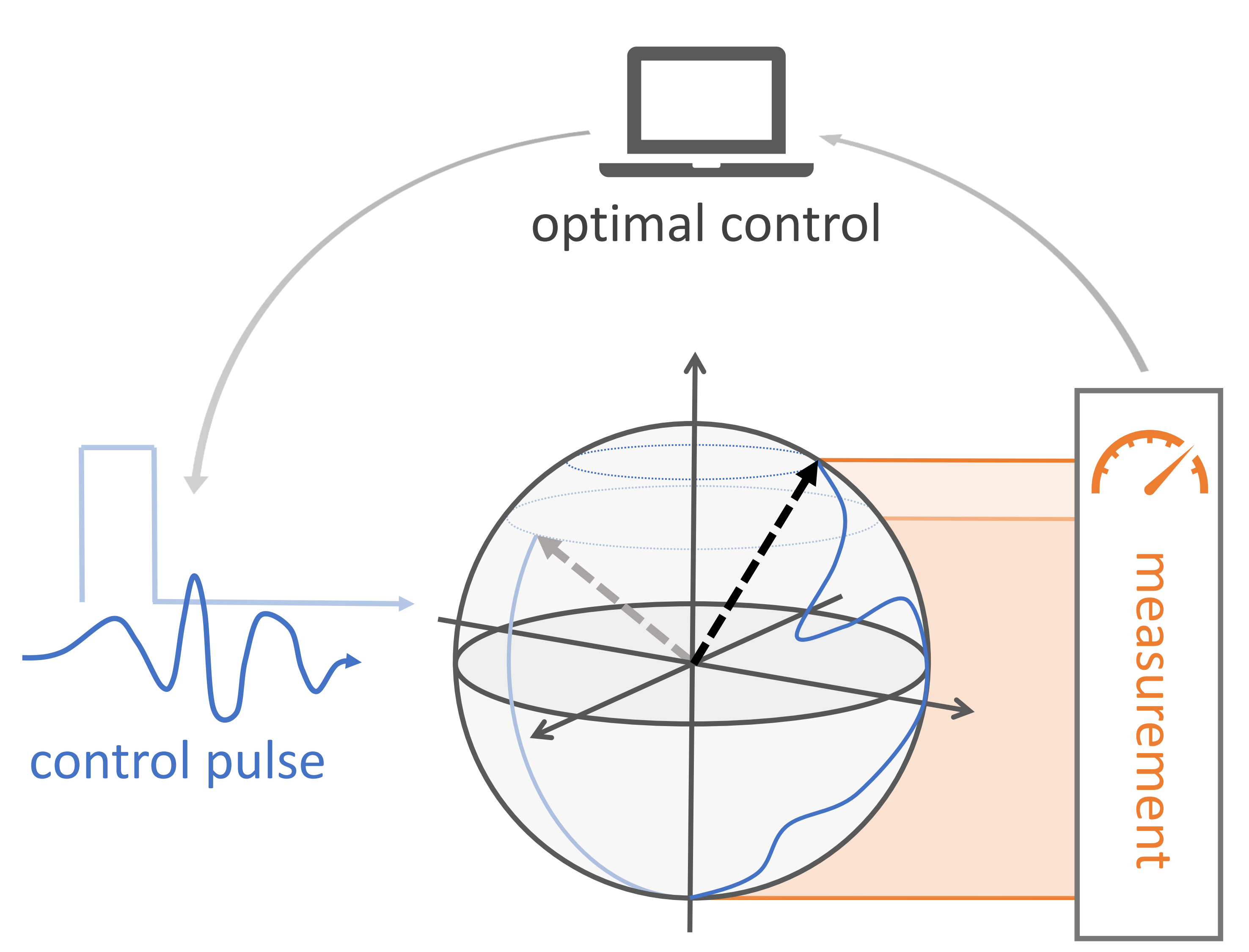
Analytical Mechanics in Optimal Control Theory
Advisor: Prof. Tirthasankar Ray, Department of Physics, IIT Kharagpur | -
I worked on this project as a part of the course Classical Mechanics-2 taught in 5th semester. Lagrangian, Hamiltonian and Hamilton-Jacobi equations of motion evolve from the optimization of the action functional over time. Optimal control policies also stem from different methods of optimization of cost over trajectory spaces with different cost functions used for different scenarios. So to optimally control a system, with known dynamics, an optimal control policy is designed through equations similar to Hamiltonian equations(given by Pontryagin’s principle). Linear Quadratic Regulator is derived through this principle also coded and tested to control an autonomously driven car on a simulator.

Monte Carlo simulations of 2D magnetic materials
Advisor: Prof. Vishwanath Shukla, Department of Physics, IIT Kharagpur | -
The 2D Ising Model and XY-model were studied numerically using the Monte-Carlo simulation using Metropolis Algorithm. The critical temperature and the effect of external field were found in these systems while to speed up the codes, MPI parallel programming was used. The project was a part of Computational Methods course taught in 5th semester.
 |
 |
|
|
|

Relativistic Evolution of Synchrotron Radiation
Advisor: Prof. Jyotirmoy Bhattacharya, Department of Physics, IIT Kharagpur | -
When electrons revolve at relativistic speeds, the radiation spectrum emitted is called the synchrotron radiation. The mathematical treatment using the Lienard-Wiechart equations is algebraically tedious and conceals the physical picture of the cyclotron to synchtron transition. In this essay, I use relativistic arguments instead to deduce various features like the angular and the spectral dispersion of synchrotron radiation field using cyclotron radiation as the basis.